OpenGL 参数方程绘制球

发表于 分类于 阅读次数： Waline：

在OpenGL中用参数方程绘制球体

效果图

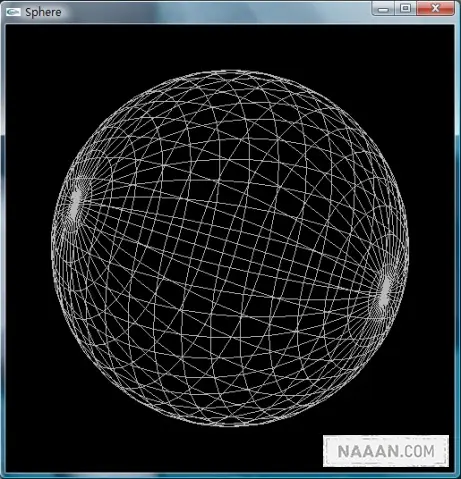
请输入图片描述

程序的代码

1
2
3
4
5
6
7
8
9
10
11
12
Sphere.h
   #pragma once
  
   // Windows Header Files
   #include <windows.h>
  
   // C RunTime Header Files
   #include <stdlib.h>
   #include <malloc.h>
   #include <memory.h>
   #include <tchar.h>
   #include <math.h>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
Sphere.h
   #include "Sphere.h"
   #include <glut.h>
  
   #define pi 3.1415926
   #define SOLID 3000
   #define WIRE  3001
  
   typedef int SPHERE_MODE;
  
   typedef struct Point3f
   {
    GLfloat x;
    GLfloat y;
    GLfloat z;
   }point;
  
   void init(void);
   void reshape(int w,int h);
   void display(void);
   int getPoint(GLfloat radius,GLfloat a,GLfloat b,point &p);
   void drawSlice(point &p1,point &p2,point &p3,point &p4,SPHERE_MODE mode);
   point* getPointMatrix(GLfloat radius,GLint slices);
   int drawSphere(GLfloat radius,GLint slices,SPHERE_MODE mode);
  
   int APIENTRY _tWinMain(HINSTANCE hInstance,HINSTANCE hPrevInstance,LPTSTR lpCmdLine,int nCmdShow)
   {
    glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
    glutInitWindowSize (500, 500);
    glutInitWindowPosition (100, 100);
    glutCreateWindow("Sphere");
    init ();
    glutReshapeFunc(reshape);
    glutDisplayFunc(display);
    glutMainLoop();
    return 0;
   }
   void init (void)
   {
    glClearColor (0.0, 0.0, 0.0, 0.0);
    glClearDepth(1);
    glShadeModel(GL_SMOOTH);
    GLfloat _ambient[]={1.0,1.0,1.0,1.0};
    GLfloat _diffuse[]={1.0,1.0,1.0,1.0};
    GLfloat _specular[]={1.0,1.0,1.0,1.0};
    GLfloat _position[]={200,200,200,0};
    glLightfv(GL_LIGHT0,GL_AMBIENT,_ambient);
    glLightfv(GL_LIGHT0,GL_DIFFUSE,_diffuse);
    glLightfv(GL_LIGHT0,GL_SPECULAR,_specular);
    glLightfv(GL_LIGHT0,GL_POSITION,_position);
    glEnable(GL_TEXTURE_2D);
    glEnable(GL_LIGHTING);
    glEnable(GL_LIGHT0);
    glEnable(GL_DEPTH_TEST);
    glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);
   }
   void reshape(int w, int h)
   {
    glViewport (0, 0, (GLsizei) w, (GLsizei) h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    glOrtho(0.0, 500, 0.0, 500, -500, 500);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
   }
   void display(void)
   {
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    glClear (GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
    glTranslated(250,250,0);
    glRotated(30,1,0,0);
    glRotated(60,0,1,0);
    glRotated(90,0,0,1);
    glColor3f(1.0,1.0,1.0);
    drawSphere(200,20,WIRE);
    glFlush();
   }
   int getPoint(GLfloat radius,GLfloat a,GLfloat b,point &p)
   {
    p.x=radius*sin(a*pi/180.0)*cos(b*pi/180.0);
    p.y=radius*sin(a*pi/180.0)*sin(b*pi/180.0);
    p.z=radius*cos(a*pi/180.0);
    return 1;
   }
   void drawSlice(point &p1,point &p2,point &p3,point &p4,SPHERE_MODE mode)
   {
    switch(mode)
    {
    case SOLID:
     glBegin(GL_QUADS);
     break;
    case WIRE:
     glBegin(GL_LINE_LOOP);
     break;
    }
    glColor3f(1,0,0);
    glVertex3f(p1.x,p1.y,p1.z);
    glVertex3f(p2.x,p2.y,p2.z);
    glVertex3f(p3.x,p3.y,p3.z);
    glVertex3f(p4.x,p4.y,p4.z);
    glEnd();
   }
   point* getPointMatrix(GLfloat radius,GLint slices)
   {
    int i,j,w=2*slices,h=slices;
    float a=0.0,b=0.0;
    float hStep=180.0/(h-1);
    float wStep=360.0/w;
    int length=w*h;
    point *matrix;
    matrix=(point *)malloc(length*sizeof(point));
    if(!matrix)return NULL;
    for(a=0.0,i=0;i<h;i++,a+=hStep)
     for(b=0.0,j=0;j<w;j++,b+=wStep) 
      getPoint(radius,a,b,matrix[i*w+j]);
    return matrix;
   }
   int drawSphere(GLfloat radius,GLint slices,SPHERE_MODE mode)
   {
    int i=0,j=0,w=2*slices,h=slices;
    point *mx;
    mx=getPointMatrix(radius,slices);
    if(!mx)return 0;
    for(;i<h-1;i++)
    {
     for(j=0;j<w-1;j++)
      drawSlice(mx[i*w+j],mx[i*w+j+1],mx[(i+1)*w+j+1],mx[(i+1)*w+j],mode);
     drawSlice(mx[i*w+j],mx[i*w],mx[(i+1)*w],mx[(i+1)*w+j],mode);
    }
    free(mx);
    return 1;
   }

首先要声明的是如果想运行上面的程序，在你的计算机上必须装有GLUT开发工具，并要将GLUT的头文件和库文件添加到你开发环境的头文件和库文件的目录中，并且让编译器能找到GLUT的动态连接库，即GLUT32.DLL。具体请参见GLUT的安装方法……

进入正题：

1 头文件

先是Sphere.h，包含了windows.h头文件和一些其他可能用到的标准C头文件，可以直接写到Sphere.cpp里面。接下来在Sphere.cpp里面包含Sphere.h和GLUT的头文件glut.h

2 自定义宏、类型和结构体

1
#define pi 3.1415926

定义圆周率pi，后面计算坐标时要用到

1
2
#define SOLID 3000
#define WIRE  3001

定义画球的模式，SOLID表示画实面球，WIRE表示画网格球

1
typedef int SPHERE_MODE;

定义画球模式的类型，其实是个int整形

1
2
3
4
5
6
typedef struct Point3f
   {
    GLfloat x;
    GLfloat y;
    GLfloat z;
   }point;

定义记录空间点坐标的结构体point，GLfloat类型其实就是GLUT里面定义的float类型

3 函数声明和实现

1
2
3
4
5
6
7
void init(void);
void reshape(int w,int h);
void display(void);
int getPoint(GLfloat radius,GLfloat a,GLfloat b,point &p);
void drawSlice(point &p1,point &p2,point &p3,point &p4,SPHERE_MODE mode);
point* getPointMatrix(GLfloat radius,GLint slices);
int drawSphere(GLfloat radius,GLint slices,SPHERE_MODE mode);

init()、reshape()和display()这3个函数是OpenGL绘图的一般过程所用的函数，这3个函数的函数名可以不同，但形参部分的形参类型必须一样（注），且这3个函数在主函数中是依次调用的。

（注： void reshape(int w,int h); 也可作 void resizeWindow(int width,int height)）

在init()函数里，分别对屏幕背景颜色，投影模式，光照，光原位置等进行了设置，并启用纹理，灯光和深度测试；

reshape()函数里面，对视口和投影矩阵进行设置；

接下来是display()函数，先移动原点坐标到窗口中心位置，再对所要绘制的图形进行一定角度的旋转，设置绘图的颜色，然后调用drawSphere()绘制球体。

关于init()，reshape()和display()这3个函数里面的具体过程，请参见OpenGL的相关教程。

下面的几个函数是绘制球体所用的，这里先简略给出他们的作用，具体实现将在下一部分详细解析：

int getPoint(GLfloat radius,GLfloat a,GLfloat b,point &p) 函数：

根据半径radius，a角（半径与Z轴正向的夹角），b角（半径在xy平面的投影与x轴正向的夹角）算出球面上点的坐标并记录到point类型的参数p中。

void drawSlice(point &p1,point &p2,point &p3,point &p4,SPHERE_MODE mode) 函数：

根据实际调用时提供的4个点的坐标在空间画四边形，并用mode参数确定所画四边形是空心还是实心的。

point* getPointMatrix(GLfloat radius,GLint slices) 函数：

根据提供的半径radius和分块数slices计算出一系列球面上的点的坐标，储存在一个动态创建的矩阵中，并返回指向该矩阵的指针，要求的分块数越多，计算的点就越多，球面就越光滑，矩阵也就越大。

int drawSphere(GLfloat radius,GLint slices,SPHERE_MODE mode) 函数：

绘球所调用的函数，根据提供的半径radius和分块数slices在窗体中绘制球体，分块数越大，球面越光滑，mode参数用于确定要绘制实面球还是网格球。

4 绘球部分

这里绘制的球，其实是个球面。把球面看成是由很多个小的四边形平面构成的，这样就可以通过绘制这些小的四边形平面来构成整个球面。而对于两极部分，需要用三角形将球面两端封起来，如果把这些三角型看作是有两个顶点重合的四边形，问题就得到进一步的简化。因此只需知道球面上一些列点的空间坐标，就可以利用这些点来绘制四边形从而得到整个球面。把整个球面展开，可见球面上这些点构成的是一个矩阵，而这个矩阵中纵横相邻的四个元素的坐标正好构成的就是球面上的一个小平面。

如何获取球面上点的坐标？

利用球的空间坐标参数方程

1
2
3
x=r·sin(α)·cos(β)
y=r·sin(α)·sin(β)
z=r·cos(α)

r是球的半径，α角是半径与Z轴正向的夹角，β角是半径在xy平面的投影与x轴正向的夹角，他们的取值范围是

1
0≤r≤∞    0≤α≤π    0≤β≤2π

因此函数 getPoint() 就是通过此参数方程来获得空间点的坐标；

1
2
3
4
5
6
7
int getPoint(GLfloat radius,GLfloat a,GLfloat b,point &p)
{
 p.x=radius*sin(a*pi/180.0)*cos(b*pi/180.0);
 p.y=radius*sin(a*pi/180.0)*sin(b*pi/180.0);
 p.z=radius*cos(a*pi/180.0);
 return 1;
}

值得注意的是 sin() 和 cos() 函数的参数是弧度角，而形参传入的是角度角，因此需要进行转换。

获取球面坐标矩阵

形参slices确定取点的间隔大小。

α角的大小是0180度，β角的大小是0360度，因此我们在z轴方向，每隔180/(slice-1)取一横列的点作为α角，在垂直于z轴的平面上，每隔360/slice取一纵列的点作为β角。由于β角的范围是α角的两倍，所以矩阵横向取点的个数是纵向取点的两倍。接下来就是动态分配内存空间，然后通过循环为矩阵中的元素，即球面上的点的坐标赋值。这里调用 getPoint() 这个函数来计算空间点坐标。虽然分配出来的空间是线性的，但可以通过元素的下标计算确定该元素在线性空间的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
point* getPointMatrix(GLfloat radius,GLint slices)
{
 int i,j,w=2*slices,h=slices;
 float a=0.0,b=0.0;
 float hStep=180.0/(h-1);
 float wStep=360.0/w;
 int length=w*h;
 point *matrix;
 matrix=(point *)malloc(length*sizeof(point));
 if(!matrix)return NULL;
 for(a=0.0,i=0;i<h;i++,a+=hStep)
  for(b=0.0,j=0;j<w;j++,b+=wStep) 
   getPoint(radius,a,b,matrix[i*w+j]);
 return matrix;
}

四点绘面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void drawSlice(point &p1,point &p2,point &p3,point &p4,SPHERE_MODE mode)
{
 switch(mode)
 {
 case SOLID:
  glBegin(GL_QUADS);
  break;
 case WIRE:
  glBegin(GL_LINE_LOOP);
  break;
 }
 glColor3f(1,0,0);
 glVertex3f(p1.x,p1.y,p1.z);
 glVertex3f(p2.x,p2.y,p2.z);
 glVertex3f(p3.x,p3.y,p3.z);
 glVertex3f(p4.x,p4.y,p4.z);
 glEnd();
}

形参mode确定了绘图的模式，当其为SOLID时，用GL_QUADS模式绘实平面，当为WIRE时，就用

GL_LINE_LOOP绘制首尾相连的四条线。注意最后要用 glEnd() 结束对该平面的绘制，否则会得到「怪异」的结果。

绘制球面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int drawSphere(GLfloat radius,GLint slices,SPHERE_MODE mode)
{
 int i=0,j=0,w=2*slices,h=slices;
 point *mx;
 mx=getPointMatrix(radius,slices);
 if(!mx)return 0;
 for(;i<h-1;i++)
 {
  for(j=0;j<w-1;j++)
   drawSlice(mx[i*w+j],mx[i*w+j+1],mx[(i+1)*w+j+1],mx[(i+1)*w+j],mode);
  drawSlice(mx[i*w+j],mx[i*w],mx[(i+1)*w],mx[(i+1)*w+j],mode);
 }
 free(mx);
 return 1;
}

这就是绘制球面的主框架函数了，先调用 getPointMatrix() 来产生球面点矩阵，并用局部变量mx记录该矩阵在内存中的位置。接下来就是把该矩阵上记录的点用 drawSlice() 函数绘成平面。例如mx[0,0]，mx[0,1]，mx[1,1]，mx[1,0]这四个元素中记录的就是沿逆时针方向构成球面上第一个平面的4个点了。要注意的是，在矩阵的横向上，最后一列点需要和第一列点连起来再绘制平面，这样产生的球面才是封闭的。在函数最后要把动态分配的内存空间释放掉，不然会造成内存泄露。如果绘制成功，函数返回1，否则返回0。

有了上面几个函数就可以在直接调用 drawSphere() 函数来绘制不同大小，不同精度和不同模式的球了。

via: http://blog.163.com/tianshi_17th/blog/static/48564189200832992845889/

The Why·Liam·Blog by WhyLiam is licensed under a Creative Commons BY-NC-ND 4.0 International License.

由WhyLiam创作并维护的Why·Liam·Blog采用创作共用保留署名-非商业-禁止演绎4.0国际许可证。

本文首发于Why·Liam·Blog (https://blog.naaln.com)，版权所有，侵权必究。

本文永久链接：https://blog.naaln.com/2013/04/opengl-parameters-equation-draw-ball/